v3.0: Three-neutrino fit based on data available in November 2016


If you are using these results please refer to JHEP 01 (2017) 087 [arXiv:1611.01514] as well as NuFIT 3.0 (2016), www.nu-fit.org.


Parameter ranges

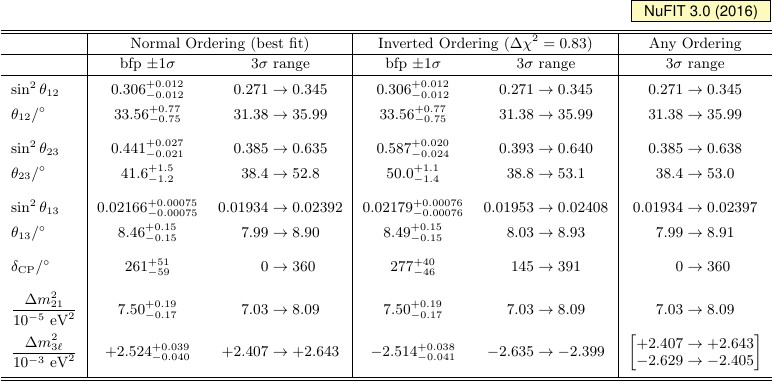
image
pdf
Three-flavor oscillation parameters from our fit to global data as of August 2016. The normalization of reactor fluxes is left free and data from short-baseline reactor experiments are included. The numbers in the 1st (2nd) column are obtained assuming NO (IO), i.e., relative to the respective local minimum, whereas in the 3rd column we minimize also with respect to the ordering. Note that Δm​23ℓ = Δm​231 > 0 for NO and Δm​23ℓ = Δm​232 < 0 for IO.


Leptonic mixing matrix

image
pdf
3σ CL ranges of the magnitude of the elements of the three-flavor leptonic mixing matrix under the assumption of the matrix U being unitary. The normalization of reactor fluxes is left free and data from short-baseline reactor experiments are included. The ranges in the different entries of the matrix are correlated due to the fact that, in general, the result of a given experiment restricts a combination of several entries of the matrix, as well as to the constraints imposed by unitarity. As a consequence choosing a specific value for one element further restricts the range of the others.


Two-dimensional allowed regions

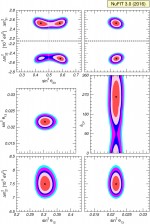
image
pdf jpg 		Global 3ν oscillation analysis. Each panel shows the two-dimensional projection of the allowed six-dimensional region after marginalization with respect to the undisplayed parameters. The different contours correspond to the two-dimensional allowed regions at 1σ, 90%, 2σ, 99%, 3σ CL (2 dof). The normalization of reactor fluxes is left free and data from short-baseline reactor experiments are included. Note that as atmospheric mass-squared splitting we use Δm​231 for NO and Δm​232 for IO. The regions in the lower 4 panels are based on a Δχ2 minimized with respect to the mass ordering.


One-dimensional χ2 projections

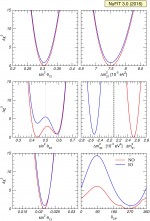
image
pdf jpg 		Global 3ν oscillation analysis. The red (blue) curves are for Normal (Inverted) Ordering. The normalization of reactor fluxes is left free and data from short-baseline reactor experiments are included. Note that as atmospheric mass-squared splitting we use Δm​231 for NO and Δm​232 for IO.


Impact of Super-K atmospheric data

image
pdf jpg 		Impact of our re-analysis of SK atmospheric neutrino data on the determination of sin2θ23, δCP, and the mass ordering. The impact on all other parameters is negligible. The red (blue) curves are for Normal (Inverted) Ordering; dashed (solid) lines include (omit) Super-K data. The normalization of reactor fluxes is left free and data from short-baseline reactor experiments are included.


CP-violation: Jarlskog invariant

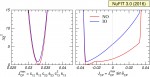
image
pdf jpg 		Dependence of Δχ2 on the Jarlskog invariant. The red (blue) curves are for NO (IO). The normalization of reactor fluxes is left free and data from short-baseline reactor experiments are included.


CP-violation: unitarity triangle

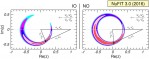
image
pdf jpg 		Leptonic unitarity triangle for the first and third columns of the mixing matrix. After scaling and rotating each triangle so that two of its vertices always coincide with (0,0) and (1,0), we plot the 1σ, 90%, 2σ, 99%, 3σ CL (2 dof) allowed regions of the third vertex. The contours for Normal (right) and Inverted (left) ordering are defined with respect to the common global minimum. The normalization of reactor fluxes is left free and data from short-baseline reactor experiments are included. Note that in the construction of the triangles the unitarity of the U matrix is always explicitly imposed.


Tension between Solar and KamLAND data

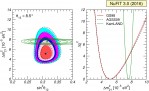
image
pdf jpg 		Left: Allowed parameter regions (at 1σ, 90%, 2σ, 99%, 3σ CL for 2 dof) from the combined analysis of solar data for GS98 model (full regions with best fit marked by black star) and AGSS09 model (dashed void contours with best fit marked by a white dot), and for the analysis of KamLAND data (solid green contours with best fit marked by a green star) for fixed θ13 = 8.5°. Right: Δχ2 dependence on Δm​221 for the same three analysis after marginalizing over θ12.


Synergies: atmospheric mass-squared splitting

image
pdf jpg 		Determination of Δm​23ℓ at 1σ and 2σ (2 dof), where ℓ = 1 for NO (upper panels) and ℓ = 2 for IO (lower panels). The left panels show regions in the (sin2θ23, Δm​23ℓ) plane using both appearance and disappearance data from MINOS (green), NOνA (cyan) and T2K (red), as well as DeepCore atmospheric data (orange) and a combination of them (colored regions). Here a prior on θ13 is included to account for reactor bounds. The right panels show regions in the (sin2θ13, Δm​23ℓ) plane using data from Daya-Bay (black), reactor data without Daya-Bay (violet), and their combination (colored regions). In all panels solar and KamLAND data are included to constrain Δm​221 and θ12. Contours are defined with respect to the global minimum of the two orderings.


Synergies: determination of Δm​23ℓ

image
pdf jpg 		Bounds on Δm​23ℓ from reactor experiments (black) as well as Minos (green), NOνA (cyan), T2K (red) and all LBL data (blue). Left (right) panels are for IO (NO); for each experiment Δχ2 is defined with respect to the global minimum of the two orderings. The upper panels show the 1-dimensional Δχ2 from LBL accelerator experiments after imposing a prior on θ13 to account for reactor bounds. The lower panels show the corresponding determination when the full information of LBL and reactor experiments is used in the combination.


Synergies: determination of θ23

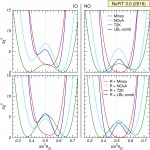
image
pdf jpg 		Bounds on θ23 from Minos (green), NOνA (cyan), T2K (red) and their combination (blue). Left (right) panels are for IO (NO); for each experiment Δχ2 is defined with respect to the global minimum of the two orderings. The upper panels show the 1-dimensional Δχ2 from LBL accelerator experiments after imposing a prior on θ13 to account for reactor bounds. The lower panels show the corresponding determination when the full information of LBL and reactor experiments is used in the combination.


Synergies: determination of δCP

image
pdf jpg 		Bounds on δCP from Minos (green), NOνA (cyan), T2K (red) and their combination (blue). Left (right) panels are for IO (NO); for each experiment Δχ2 is defined with respect to the global minimum of the two orderings. The upper panels show the 1-dimensional Δχ2 from LBL accelerator experiments after imposing a prior on θ13 to account for reactor bounds. The lower panels show the corresponding determination when the full information of LBL and reactor experiments is used in the combination.


Correlation between δCP and other parameters

image
pdf jpg 		Allowed regions from the global data at 1σ, 90%, 2σ, 99%, 3σ CL (2 dof) after minimizing with respect to all undisplayed parameters. The normalization of reactor fluxes is left free and data from short-baseline reactor experiments are included. The upper (lower) panel corresponds to IO (NO). Note that as atmospheric mass-squared splitting we use Δm​231 for NO and Δm​232 for IO.


Monte-Carlo: confidence levels on δCP

image
pdf jpg 		68%, 95% and 99% confidence levels on δCP (broken curves) obtained from a Monte Carlo simulation of LBL and reactor data, together with the observed Δχ2 (solid lines). The value of θ23 given in each panel corresponds to the assumed true value chosen to generate the pseudo-experiments. For all panels we take Δm​232 = -2.53×10-3 eV2 for IO and Δm​231 = +2.54×10-3 eV2 for NO. The solid horizontal lines represent the 68%, 95% and 99% CL predictions from Wilks' theorem.


Monte-Carlo: confidence levels on θ23

image
pdf jpg 		68%, 95% and 99% confidence levels on θ23 (broken curves) obtained from a Monte Carlo simulation of LBL and reactor data, together with the observed Δχ2 (solid lines). The value of δCP given in each panel corresponds to the assumed true value chosen to generate the pseudo-experiments. For all panels we take Δm​232 = -2.53×10-3 eV2 for IO and Δm​231 = +2.54×10-3 eV2 for NO. The solid horizontal lines represent the 68%, 95% and 99% CL predictions from Wilks' theorem.


Available data files

We provide one- and two-dimensional Δχ2 projections for both Normal and Inverted Ordering. A description of the content of these files and a summary of the data included in our analysis can be found here.
»